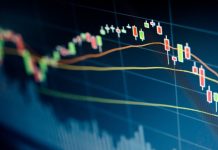
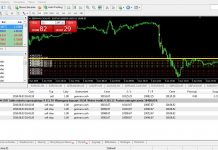
Metoda na obliczanie logarytmicznej stopy zwrotu. Wzór na nią jest to iloraz dwóch składników (wartości obecnej oraz kapitału początkowego).Z uzyskanej wartości należy obliczyć logarytm naturalny (o podstawie e, czyli tzw. liczby Eulera, wynoszącej w przybliżeniu 2,72).
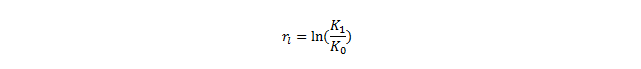
Gdzie:
- rl – logarytmiczna stopa zwrotu z akcji
- Kl – cena instrumentu finansowego
Obliczenie logarytmicznej stopy zwrotu w pamięci jest praktycznie niemożliwe, jednak z pomocą przychodzi arkusz kalkulacyjny (np. MS Excel), w którym posługując się funkcją LN() możemy obliczyć tę wartość dla powyższego przykładu. Przybliżony do dwóch miejsc po przecinku wynik 22,31% wskazuje, że wartości zwykłej i logarytmicznej stopy zwrotu są z jednej strony podobne, a z drugiej nie są sobie równe.
Zwykła stopa zwrotu
Jedną z głównych cech charakteryzującą dobrą inwestycje jest wysoka stopa zwrotu. W praktyce oznacza to, że zainwestowane pieniądze wygenerowały wysoki dochód. W matematyce finansowej wyróżniamy dwa rodzaje tego miernika…
Zwykła stopa zwrotu (rate of return, asset return):
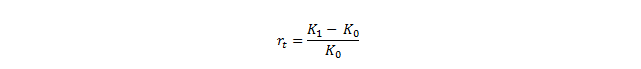
- Rt – zwykła stopa zwrotu (np. z akcji),
- K1 – wartość kapitału po upływie okresu inwestycji,
- K0 – wartość kapitału zainwestowanego.
Przykład zwykłej stopy zwrotu
Jeśli zakupiono walor za kwotę 2000 zł (K0), a po pewnym czasie sprzedano go za 2500 zł (K1), wówczas zwykła stopa zwrotu będzie ilorazem 500 oraz 2000 zł. Wynik 25% oznacza, że zainwestowane pieniądze wygenerowały zysk w wysokości 25% kapitału początkowego.