Problem ze średnią

Z uwagi na prostotę takiego rozwiązania, wielu graczy ocenia statystyczne osiągnięcia zawodników na podstawie średniej. Ale ilu z nich zdaje sobie sprawę z jej ograniczeń?

Przeanalizujmy zakłady na sumę bramek w meczu piłkarskim. Wydawałoby się, średnia liczba bramek we wcześniejszych meczach może być wyznacznikiem spodziewanego wyniku w meczach późniejszych. Ale czy średnia rzeczywiście jest miarodajnym wskaźnikiem?

Zabezpiecz się w razie niekorzystnych wyników. Sprawdź, jakie bonusy oferuje bukmacher.

„Średnia daje nam ogólny obraz sytuacji, ale nie uwzględnia rozkładu wyników”

Przyjrzyjmy się liczbie bramek strzelonych w sezonie 2013/14 La Ligi i Premier League. Średnia wyniosła odpowiednio 2,77 i 2,75 bramki na mecz. Mogłoby się zatem wydawać, że wyniki poniżej 2,5 bramki padały częściej w La Lidze niż w EPL. Rzeczywistość pokazuje jednak coś innego. W EPL 48,4% meczów skończyło się wynikiem poniżej 2,5 bramki, podczas gdy w La Lidze odsetek ten wyniósł 47,3%.

Poniższy wykres jasno pokazuje, że mimo podobnego rozkładu wartości, mecze Premier League najczęściej kończyły się dwiema bramkami, a La Ligi – trzema. Średnia uniemożliwia nam dostrzeżenie tego faktu.

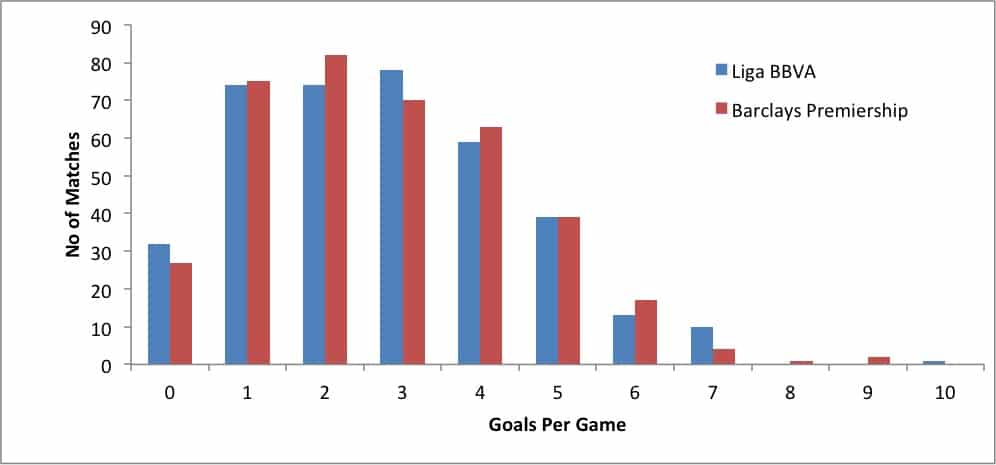
Dlaczego tak jest? Średnia daje nam ogólny obraz sytuacji, ale nie uwzględnia rozkładu wyników.

Kolejny obszar, w którym średnia może okazać się zdradliwa, są handicapy na słabsze zespoły w turniejach międzynarodowych piłki nożnej, uważane często za „chłopców do bicia” fazy kwalifikacyjnej. Ale czy rzeczywiście są one aż tak słabe? Wyciągnięcie średniej liczby bramek na mecz najprawdopodobniej przyniesie nam bardzo wysokie wyniki, należy jednak pamiętać, że mogą one być przekłamane przez niezbyt częste, ale bardzo dotkliwe porażki. W rezultacie możemy popaść w przesadny optymizm w kwestii spodziewanej liczby bramek.

Poniżej omawiamy alternatywy dla średniej arytmetycznej – dominantę i medianę – oraz przedstawiamy trzy zbiory liczb, które pokażą nam, kiedy średnia może okazać się zwodnicza.

Weźmy pod uwagę następujące liczby. Średnia każdego zbioru wynosi pięć.

• Zbiór A: 4, 5, 5, 5, 6
• Zbiór B: 3, 4, 4, 4, 10
• Zbiór C: 3, 4, 5, 6, 7

Pierwszy scenariusz: elementy odstające na niższym/wyższym końcu

Mimo że średnia liczb we wszystkich zbiorach jest identyczna, a ich suma zawsze wynosi 25, ich rozkład jest bardzo zróżnicowany.

Zbiór A możemy uznać za symetryczny. Na obu granicach średniej znajduje się jedna liczba – 4 poniżej i 6 powyżej.

Średnia sprawdza się właśnie w przypadku zbiorów symetrycznych, czyli takich, w których określone wartości zmiennych pojawiają się z podobną częstotliwością na obu granicach średniej, a średnia leży pośrodku.

Natomiast w zbiorze B mamy aż cztery liczby poniżej średniej i tylko jedną powyżej. Jest to tak zwany rozkład skośny.

„Zrozumienie ograniczeń średniej pozwoli graczom lepiej ocenić jej przydatność w ocenie prawdopodobieństwa”

W przypadku większych zbiorów danych gracze mogą sprawdzić zasadność zastosowania średniej za pomocą innych narzędzi – mediany i dominanty.

Mediana to wartość leżąca pośrodku rozkładu ułożonego w kolejności rosnącej lub malejącej. W zbiorach A i B wynosi ona odpowiednio 5 i 4. Dominanta to wartość występująca najczęściej, czyli w naszym przykładzie również 5 i 4.

Rozkład symetryczny powinien charakteryzować się podobną średnią, medianą i dominantą. Różnica pomiędzy ostatnimi dwoma a średnią arytmetyczną w zbiorze B wskazuje, że jest to rozkład skośny, zatem średnia nie jest optymalnym narzędziem do jego oceny.

Drugi scenariusz: różnica rozstępu

Dwa zbiory mogą być symetryczne, ale mogą różnić się rozstępem. Na przykład, zbiory A i C są symetryczne, ponieważ posiadają równą liczbę wartości poniżej i powyżej średniej. Ponadto w obu zbiorach oba końce w równym stopniu odbiegają od średniej.

Średnia w obu zbiorach wynosi 5, jednak znacznie lepiej opisuje ona zbiór A, ponieważ zawiera on więcej bliskich jej wartości. Różnica pomiędzy zbiorami leży w tak zwanym rozrzucie. Spróbujmy go zmierzyć.

Aby zmierzyć rozrzut, należy obliczyć rozstęp i odchylenie standardowe. Rozstęp to różnica pomiędzy największą i najmniejszą wartością w zbiorze. Jego obliczanie nie należy do trudnych. Natomiast odchylenie standardowe może przysporzyć odrobinę więcej problemów. Upraszczając dla celów niniejszego artykułu, jest to odchylenie wartości w zbiorze danych od średniej. Pracujemy nad artykułem, który bardziej szczegółowo poruszy kwestię rozkładu. Tam też napiszemy więcej na temat odchylenia standardowego.

Rozstęp w zbiorach A i C wynosi odpowiednio 2 i 4, natomiast odchylenie standardowe – 0,71 i 1,58. Ponieważ oba wyniki są znacznie wyższe w zbiorze C, możemy stwierdzić, że występuje w nim dużo większa różnorodność.

Podsumowanie

Zrozumienie ograniczeń średniej (rozkładów skośnych i różnic w rozrzucie) pozwala graczom lepiej ocenić jej przydatność w ocenie prawdopodobieństwa. Mimo że niniejszy artykuł nie analizuje tej kwestii szczegółowo, powinien wystarczyć jako ostrzeżenie i zachęta do rozważenia innych narzędzi.

Zależy ci na obniżeniu ryzyka zakładów? Sprawdź, kiedy warto wybrać bukmachera DNB.