Wiedza na temat złotego podziału miała duże znaczenie również dla twórczości artystycznej. Fascynacja nim była szczególnie silna w starożytnym Egipcie i Grecji, a także podczas renesansu, czyli w okresach wielkiej świetności cywilizacji ludzkiej. Wielką wagę do tych proporcji przywiązywał Leonardo Da Vinci. On także uznawał je za przyjemne dla człowieka i mówił, że jeśli coś nie ma właściwego wyglądu, to nie oddziałuje”. Wiele jego obrazów miało ów właściwy wygląd, ponieważ da Vinci posługiwał się złotym podziałem dla zwiększenia ich mocy oddziaływania.
Wprawdzie artyści i architekci posługiwali się świadomie złotym podziałem stosując własne kanony artystyczne, ale proporcje wyrażone przez phi najwyraźniej rzeczywiście mają wpływ na odbiorców. Przeprowadzono pewne eksperymenty, które wykazały, że ludzie uważają te proporcje za estetyczne.. Badani mieli wybrać jeden z bardzo wielu różnych prostokątów i wybór ich padał na ogół na kształt zbliżony do złotego prostokąta. Kiedy mieli w dowolny sposób skrzyżować dwa odcinki, także dokonywali tego na ogół w proporcjach wyznaczanych przez phi. Również okna, ramy do obrazów, budowle, książki i nagrobki cmentarne często są w przybliżeniu złotymi prostokątami.
Przeczytaj więcej : Poziomy (zniesienia Fibonacciego)
Znaczenie złotych proporcji nie ogranicza się do estetycznego piękna, lecz wiąże się również z określonymi funkcjami praktycznymi. Pośród wielu przykładów szczególnie znamiennym jest to, że podwójny łańcuch DNA tworzy precyzyjne złote podziały w regularnych odstępach swoich splotów.
Podczas gdy złoty podział i złoty prostokąt są statycznymi postaciami estetycznego piękna i funkcji tworzonymi przez przyrodę i człowieka, to symbol estetycznego dynamizmu i wyraz uporządkowanego rozwoju lub postępu może być dziełem tylko jednej z najbardziej niezwykłych form we wszechświecie, czyli złotej spirali.
Złota spirala
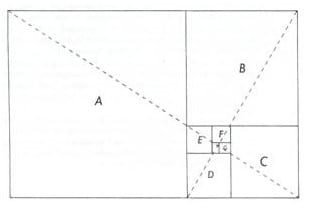
Dla skonstruowania złotej spirali można posłużyć się złotym prostokątem. Każdy złoty prostokąt można podzielić na kwadrat i mniejszy złoty prostokąt. Procedurę tę może teoretycznie kontynuować w nieskończoność. Powstające kwadraty, które jakby wirowały do wewnątrz, oznaczyliśmy A, B, C, D, E, F oraz G. Linie przerywane, które też pozostają ze sobą w złotych proporcjach, przecinają prostokąty wskazując teoretyczne centrum tego dośrodkowego ruchu. Z tego punktu możemy wytyczyć spiralę łączącą punkty styczne kolejnych coraz większych kwadratów. W ten oto sposób powstaje złota spirala. Dla jej konstrukcji można również posłużyć się sekwencją wirujących trójkątów.
W dowolnym punkcie ewolucji złotej spirali stosunek długości łuku do jego przekątnej wynosi 1,618, a przekątna pozostaje w takim stosunku do większego promienia, jak większy promień do mniejszego, czyli 1,618.
Wiedza na temat złotego podziału miała duże znaczenie również dla twórczości artystycznej. Fascynacja nim była szczególnie silna w starożytnym Egipcie i Grecji, a także podczas renesansu, czyli w okresach wielkiej świetności cywilizacji ludzkiej. Wielką wagę do tych proporcji przywiązywał Leonardo Da Vinci. On także uznawał je za przyjemne dla czło-wieka i mówił, że jeśli coś nie ma właściwego wyglądu, to nie oddziałuje”. Wiele jego obrazów miało ów właściwy wygląd, ponieważ da Vinci posługiwał się złotym podziałem dla zwiększenia ich mocy oddziaływania.
Wprawdzie artyści i architekci posługiwali się świadomie złotym podziałem stosując własne kanony artystyczne, ale proporcje wyrażone przez phi najwyraźniej rzeczywiście mają wpływ na odbiorców. Przeprowadzono pewne eksperymenty, które wykazały, że ludzie uważają te proporcje za estetyczne.. Badani mieli wybrać jeden z bardzo wielu różnych prostokątów i wybór ich padał na ogół na kształt zbliżony do złotego prostokąta. Kiedy mieli w dowolny sposób skrzyżować dwa odcinki, także dokonywali tego na ogół w proporcjach wyznaczanych przez phi. Również okna, ramy do obrazów, budowle, książki i nagrobki cmentarne często są w przybliżeniu złotymi prostokątami.
Znaczenie złotych proporcji nie ogranicza się do estetycznego piękna, lecz wiąże się również z określonymi funkcjami praktycznymi. Pośród wielu przykładów szczególnie znamiennym jest to, że podwójny łańcuch DNA tworzy precyzyjne złote podziały w regularnych odstępach swoich splotów.
Podczas gdy złoty podział i złoty prostokąt są statycznymi postaciami estetycznego piękna i funkcji tworzonymi przez przyrodę i człowieka, to symbol estetycznego dynamizmu i wyraz uporządkowanego rozwoju lub postępu może być dziełem tylko jednej z najbardziej niezwykłych form we wszechświecie, czyli złotej spirali.
Złota spirala
Dla skonstruowania złotej spirali można posłużyć się złotym prostokątem. Każdy złoty prostokąt można podzielić na kwadrat i mniejszy złoty prostokąt. Procedurę tę może teoretycznie kontynuować w nieskończoność. Powstające kwadraty, które jakby wirowały do wewnątrz, oznaczyliśmy A, B, C, D, E, F oraz G. Linie przerywane, które też pozostają ze sobą w złotych proporcjach, przecinają prostokąty wskazując teoretyczne centrum tego dośrodkowego ruchu. Z tego punktu możemy wytyczyć spiralę łączącą punkty styczne kolejnych coraz większych kwadratów. W ten oto sposób powstaje złota spirala. Dla jej konstrukcji można również posłużyć się sekwencją wirujących trójkątów.
W dowolnym punkcie ewolucji złotej spirali stosunek długości łuku do jego przekątnej wynosi 1,618, a przekątna pozostaje w takim stosunku do większego promienia, jak większy promień do mniejszego, czyli 1,618.
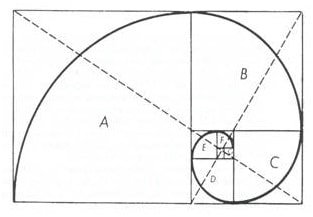
Złota spirala, która jest spiralą logarytmiczną lub równokątną, nie ma żadnych granic, choć ma stały kształt. Z dowolnego punktu spirali można podążać w nieskończoność zarówno dośrodkowo, jak i odśrodkowo. Nigdy nie można dotrzeć do środka i także na zewnątrz nie ma żadnego ograniczenia. Jądro spirali logarytmicznej widziane przez mikroskop wyglądałoby tak samo jak jej najszersza część mierzona w latach świetlnych. Jak zauważył David Bergamini w Mathematics (Time–Life Books’ Science Library), ogon komety odchyla się od Słońca w postaci logarytmicznej spirali; na kształt takiej spirali snuje swą sieć pająk epeira; bakterie rozmnażają się w tempie, które można nanieść na spiralę logarytmiczną; meteoryty, kiedy uderzają o powierzchnię Ziemi, powodują wgłębienia odpowiadające spirali logarytmicznej. Szyszki sosny, koniki morskie, muszle ślimaków i mięczaków, fale oceanu, paprocie, rogi zwierzęce, nasiona słonecznika i stokrotki również tworzą spirale logarytmiczne. Chmury huraganowe i galaktyki skręcone są w kształcie spirali logarytmicznej. Nawet palec człowieka, składający się z trzech kości pozostających ze sobą w złotych proporcjach, przybiera po zgięciu spiralny kształt przypominający zwiędły liść poinsecji. Na diagramach widzimy odzwierciedlenie tego kosmicznego wpływu w wielu postaciach. Szyszkę sosny i spiralę galaktyczną oddzielają eony czasu i lata świetlne przestrzeni, ale schemat jest ten sam: współ-czynnik 1,618, stanowiący być może najważniejszą zasadę rozwoju zjawisk przyrodniczych. A zatem złota spirala rozpościera się w symbolicznej postaci jako jeden ze wspaniałych wzorów natury, obraz życia w nieustannej ekspansji i cofaniu się, statyczne prawo rządzące dynamicznym procesem oparte na złotym współczynniku 1,618.
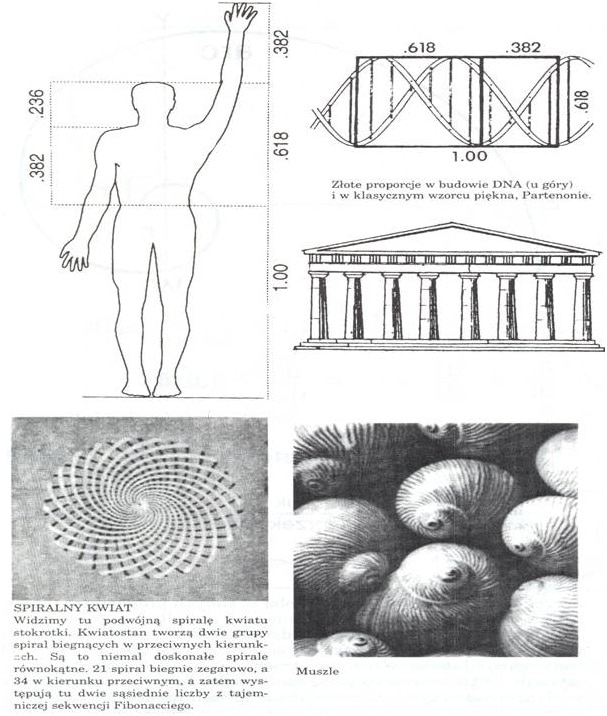

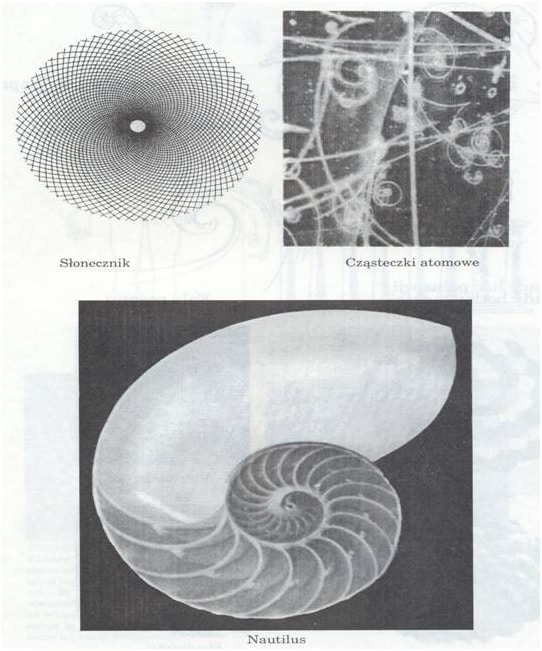
Przykłady złotych spirali w przyrodzie (Alfred J. Frost, Robert E. Prechter. Teoria fal Elliotta. WIG-Press Warszawa 1995, s. 94)

Znaczenie liczby Phi
Znaczenie tego wszechobecnego fenomenu było rozumiane i doceniane przez największe umysły różnych epok. Historia zna wiele przykładów uczonych mężów, którzy w szczególny sposób zafascynowani byli tą matematyczną formułą. Najwcześniejszy przykład i jeden z najbardziej interesujących dotyczy architektów egipskiej piramidy w Gizie, którzy blisko 5000 lat temu wykazali się wiedzą na temat złotych proporcji. Inżynierowie egipscy świadomie uwiecznili je po wsze czasy w konstrukcji piramidy nadając nachylonym ścianom tej budowli wysokość równą 1,618 połowy jej podstawy, w rezultacie czego wysokość samej piramidy w pionie jest zarazem pierwiastkiem kwadratowym z 1,618 pomnożonym przez połowę jej podstawy. Posługując się tymi proporcjami egipscy uczeni (prawdopodobnie w celu zbudowania modelu półkuli północnej) zastosowali pi i phi w metodzie tak zaawansowanej matematycznie, że umożliwiała ona wyliczenie kwadratu koła i sześcianu kuli (tzn. nadanie im równej powierzchni i objętości), czego nie zdołano powtórzyć przez ponad cztery tysiące lat.
Ci, którzy projektowali i budowali piramidy, byli świetnymi uczonymi, astronomami, matematykami i inżynierami. Najwyraźniej chcieli oni uwiecznić złote proporcje jako coś, co ma znaczenie transcendentne. Fakt, że ludzie tej miary, a później największe umysły Grecji i okresu Oświecenia, zafascynowani byli tym współczynnikiem, jest istotny już sam w sobie. Na pytanie dlaczego tak się działo, możemy odpowiedzieć jedynie odwołując się do przypuszczeń kilku badaczy. Istniało na przykład domniemanie, że wielka piramida przez całe stulecia służyła jako świątynia inicjacji dla tych, którzy okazali się godni zrozumienia największych sekretów wszechświata. Tylko ci, którzy potrafili wznieść się ponad potoczne doświadczenie i pozorny obraz rzeczy, aby odkryć ich prawdziwą istotę, mogli dostąpić wtajemniczenia w prawdy dotyczące wiecznego porządku i rozwoju wszechświata. Czy pośród tych „tajemnic” był również współczynnik phi? Tompkins twierdzi, że „w Egipcie faraonów, zdaniem Schwallera de Lubicza, phi nie było traktowane jako liczba, lecz jako symbol funkcji kreatywnej, czyli nie kończącej się reprodukcji. Był to symbol „życiowego ognia, męskiej płodności, logosu z Ewangelii św. Jana””. Greckie słowo logos było na różne sposoby defi-niowane przez Heraklita oraz późniejszych filozofów greckich, żydowskich i chrześcijańskich jako racjonalny porządek wszechświata, immanentna zasada natury, życiodajna moc ukryta w bycie, rządząca światem i przenikająca go kosmiczna siła.
Jeśli dawni filozofowie mieli rację twierdząc, że światem rządzi przenikająca go kosmiczna siła, czy nie jest tak również w przypadku świata ludzkiego? Jeśli formy istniejące we wszechświecie, w tym ludzkie ciało i mózg, odzwierciedlają phi, czy nie może być podobnie z działaniami człowieka? Jeśli phi jest życiodajną siłą kosmiczną, czy nie może ono być impulsem kryjącym się za rozwojem ludzkich zdolności twórczych? Jeśli phi jest symbolem funkcji kreatywnych, czy nie może rządzić twórczymi poczynaniami człowieka? Jeśli postęp ludzki opiera się na wytwarzaniu i „nie kończącym się” odtwarzaniu, czyż nie jest możliwe, że postęp taki ma spiralną formę phi i że formę tę znaleźć można również na rynku kapitałowym? Podobnie jak dostępujący wtajemniczenia Egipcjanie poznawali ukryte prawdy dotyczące porządku dynamicznego wszechświata kryjącego się za pozorną przypadkowością i chaosem, tak i my usiłując zrozumieć rynek kapitałowy musimy badać czym on jest, a nie czym wydaje się przy powierzchownym oglądzie. Rynek ten nie jest chaotycznym, przypadkowym czy bezkształtnym tworem reagującym na bieżące wiadomości, lecz niezwykle precyzyjnym zapisem formalnej struktury rozwoju ludzkiego.
Można porównać tę koncepcję z opinią astronoma Williama Kingslanda wyrażoną w The Great Pyramid in Fact and Theory, który twierdził, że egipska astronomia i astrologia była „nauką głęboko ezoteryczną związaną z wielkimi cyklami ewolucji człowieka”. Teoria fal wyjaśnia te wielkie cykle i pokazuje dlaczego i w jaki sposób one przebiegają. Dotyczy ona nadto zarówno cykli w skali makro, jak i mikro, bowiem wszystkie one oparte są na paradoksalnej zasadzie dynamiki i zmienności w ramach stałej formy.
Właśnie ta forma nadaje kosmosowi strukturę i jedność. Nic nie wskazuje na to, że fenomen życia jest chaotyczny czy bezkształtny. „Kosmos” oznacza „porządek”. Jeśli życie ma swoją formę, to nie wolno nam odrzucać prawdopodobieństwa, że rozwój ludzki, który jest częścią życia jako całości, również cechuje pewien porządek i forma. Siłą rzeczy, rynek, który dokonuje oceny ludzkich twórczych przedsięwzięć, także będzie cechował się porządkiem i formą. Wszystkie techniczne sposoby zrozumienia rynku oparte są na podstawowej zasadzie porządku i formy. Teoria Elliotta idzie jednak jeszcze dalej. Otóż zakłada ona, że bez względu na wielkość tej formy, podstawowy schemat pozostaje bez zmian.
Swojej drugiej pracy na temat teorii fal Elliott nadał jeszcze ambitniejszy tytuł „Prawo natury – tajemnica wszechświata” odnosząc to prawo do wszystkich rodzajów działalności człowieka. Elliott poszedł być może za daleko twierdząc, że zasada falowa jest tajemnicą wszechświata, ponieważ natura stworzyła bardzo wiele form i procesów, a nie tylko jeden prosty schemat. Mimo wszystko zarówno Pitagoras, który przyjął pięcioramienną gwiazdę z jej naturalnymi złotymi podziałami jako symbol swego bractwa, jak też Isaac Newton, który na wezgłowiu łóżka miał wyrzeźbioną spiralę logarytmiczną, prawdopodobnie zgodziliby się ze sformułowaniem Elliotta.
Z pewnością można powiedzieć, że fale są jednym z najważniejszych sekretów wszechświata. Nawet to twierdzenie może wydać się wielu inwestorom ogromną przesadą, co byłoby całkiem zrozumiałe, bowiem rozmach tej koncepcji stanowi poważne wyzwanie dla ludzkiej wyobraźni i intelektu. Czy rzeczywiście istnieje taka zasada, która funkcjonuje w oparciu o te same podstawy matematyczne „w niebie i na ziemi” i jeszcze w dodatku na rynku kapitałowym?
Odpowiedź brzmi: tak, zachowania rynku opierają się na tych samych podstawach matematycznych, co zjawiska przyrodnicze. Modelowa struktura postępu fal z koncepcji Elliotta jest doskonałą podstawą dla skonstruowania złotej spirali, co w uproszczonym ujęciu widać na rysunku 11. Szczyt każdej kolejnej fali wyższego stopnia styka się z krzywą spirali logarytmicznej.
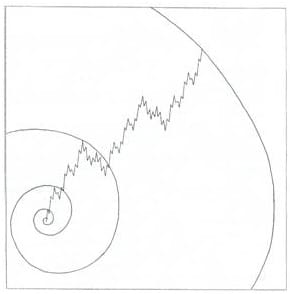
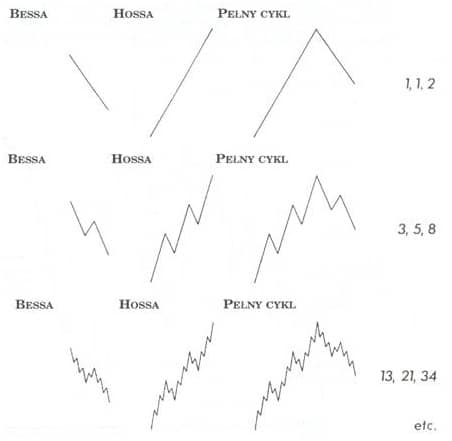
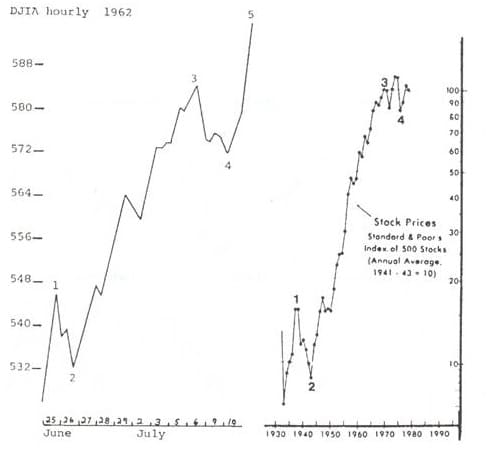
Formacje powstające na rynkach kapitałowych powtarzają się także w tym sensie, że ten sam podstawowy kształt ruchu cen, który pojawia się w mniejszych falach widocznych na wykresach godzinowych, występuje również w super cyklach i wielkich super cyklach widocznych na wykresach uwzględniających rok jako jednostkę czasu. Na rysunku 13 widzimy dwa wykresy, z których jeden (a) przedstawia godzinowe fluktuacje DJIA z okresu dziesięciu dni od 25 czerwca do 10 lipca 1962, a drugi (b) zachowanie indeksu S&P 500 w latach 1932-1978. Oba wykresy przedstawiają podobne kształty, mimo że stosunek długości tych dwóch okresów wynosi 1500 do 1. Dlaczego tak jest? Ponieważ na rynku kapitałowym forma nie jest bezwzględnie uzależniona od czynnika czasu. W myśl reguł Elliotta zarówno wykres długoterminowy, jak i krótkoterminowy, ukazuje relację 5-3, którą można odnieść do formy odzwierciedlającej własności ciągu liczb Fibonacciego. Wynika stąd, że ludzkie emocje w ich społecznej ekspresji podlegają temu matematycznemu prawu natury.
Także i strukturalny porządek fal Elliotta stanowi odzwierciedlenie ciągu liczb Fibonacciego. Mamy tu jedną podstawową formę: pięciofalową sekwencję. Istnieją dwa sposoby kształtowania się fal: fale impulsu (które dzielą się na fale kardynalne oznaczane cyframi) oraz fale korygujące (dzielące się na fale konsonansowe oznaczane literami). Są trzy klasy prostych formacji falowych: piątki, trójki oraz trójkąty (które mają cechy zarówno piątek, jak i trójek). Jest pięć rodzin prostych formacji: impulsy, trójkąty ukośne, zygzaki, fale płaskie oraz trójkąty. Mamy też trzynaście prostych formacji: impuls, trójkąt ukośny końcowy, trójkąt ukośny początkowy, zygzak, podwójny zygzak, potrójny zygzak, falę płaską regularną, falę płaską rozszerzoną, falę płaską pędzącą, trójkąt zwężający się, trójkąt zniżkujący, trójkąt zwyżkujący oraz trójkąt rozszerzający się. Fale korygujące dzielą się na dwa rodzaje porządków, to znaczy proste i złożone, co daje łącznie trzy porządki. Istnieją dwie klasy fal korygujących złożonych (podwójna i potrójna korekta), a zatem łącznie jest ich pięć. Ponieważ w myśl teorii Elliotta w korekcie złożonej może występować tylko jeden trójkąt i jeden zygzak, mamy w sumie osiem rodzin korekt złożonych: zygzak/płaska, zygzak/trójkąt, płaska/płaska, płaska/trójkąt, zygzak/ /płaska/płaska, zygzak/płaska/trójkąt, płaska/płaska/płaska oraz płaska/ /płaska/trójkąt, co daje razem trzynaście rodzin. Łącznie jest dwadzieścia jeden rodzin prostych formacji i korekt złożonych. Układ ten można dalej rozszerzać uwzględniając permutacje poszczególnych kombinacji lub kolejne odmiany struktury fal o mniejszym znaczeniu, takie jak wydłużenia, typy zmienności, obecność lub nie-obecność trójkąta ukośnego w impulsie, rodzaje trójkątów występujących w korektach złożonych itd.
Spiralna forma zachowań rynku wykazuje powtarzającą się zależność od złotego współczynnika i nawet same liczby Fibonacciego pojawiają się w statystyce rynku znacznie częściej, niż mogłoby to się zdarzać na zasadzie czystego przypadku. Przede wszystkim należy jednak zaznaczyć, że choć same liczby też mają swą teoretyczną wagę w teorii fal, to jednak właśnie proporcje są kluczem do zrozumienia schematów rozwojowych rynku. A zatem określone liczby składające się na sekwencję Fibonacciego są istotne jako wyraz matematycznej podstawy rynku, ale to proporcje wynikające z ciągu Fibonnacciego stanowią fundamentalne prawo postępu geometrycznego, w którym dwie kolejne liczby sumuje się, aby uzyskać następną. Oto dlaczego proporcje te wyznaczają tak wiele relacji w szeregach danych, które dotyczą naturalnych zjawisk rozwoju i rozpadu, ekspansji i cofania się, postępu i regresu.
W najszerszym ujęciu teoria fal zakłada, że to samo prawo, które kształtuje spiralne galaktyki w kosmosie, obecne jest w postawach i zachowaniach zbiorowości ludzkiej. Teoria Elliotta znajduje wyraźne potwierdzenie na rynku, ponieważ jest on bezwzględnie najlepszym odzwierciedleniem zbiorowej psychiki. Mamy tu niemal doskonały zapis trendów ludzkiej sytuacji społecznej i psychologicznej, który ukazuje zmieniającą się ocenę przedsięwzięć twórczych człowieka i odsłania rzeczywiste schematy rozwoju i regresu. Mamy do czynienia po prostu z empirycznymi dowodami, które są dostępne dla badań i obserwacji. Wspomniane paralele są zbyt wyraźne i znaczące, aby odrzucić je jako niedorzeczność. Ważąc prawdopo-dobieństwa dochodzi się do wniosku, że istnieje pewna wszechobecna zasada, która nadaje kształt społecznemu wymiarowi życia ludzkiego i że Einstein wiedział, co mówi, twierdząc, że „Bóg nie gra w kości”. Rynek kapitałowy nie jest pod tym względem wyjątkiem, jako że zachowania zbiorowe są bez wątpienia powiązane z prawem, które można badać i zdefiniować. Najkrótszym sposobem wyrażenia tej zasady jest prosta formuła matematyczna: stosunek 1,618.
W utworze Desiderata Maxa Ehrmanna czytamy: „Jesteś dzieckiem wszechświata tak samo jak drzewa czy gwiazdy i masz prawo tu być. Niezależnie od tego, co sądzisz na ten temat, bądź pewien, że wszechświat jest na pewno taki, jaki być powinien.”
Fenomen życia kryje w sobie pewien porządek? Rynek kapitałowy też? Tak można sądzić.
Istnieje wiele praw natury. W obecnym supercyklu ludzie stali się ślepi na jedno z nich; każda istota żyjąca w naturalnym środowisku albo zapewnia sobie środki do istnienia albo skazana jest na nieistnienie. Piękno natury polega na jej różnorodności, w której każdy żywy element spleciony jest z innymi i gdzie często jest tak, że zapewniając własne istnienie zapewnia też istnienie wielu innych. Nie ma jednak żywego stworzenia, które domagałoby się nieustannie wsparcia do swoich sąsiadów, twierdząc ze ma do tego prawo – ponieważ prawo takie nie istnieje. Każde drzewo, każdy kwiat, każdy królik i każdy wilk biorą od natury to, co daje, nie spodziewając się niczego ze strony swoich żyjących sąsiadów, wymagając czegoś od nich naruszyłoby ich piękno, a wraz z nim piękno całej rozwijającej się natury. Jednym z najszlachetniejszych eksperymentów w dziejach człowieka był amerykański system ludzkiej wolności wraz z jego nieodzownym środowiskiem, jakim jest oparty na wolnej konkurencji kapitalizm. Idea ta uwolniła człowieka od więzów narzucanych przez innych: panów feudalnych, dziedziców, królów, biskupów, biurokratów, a także związków zawodowych domagających się darmowego chleba i igrzysk. Różnorodność, bogactwo i piękno tego eksperymentu zapisały się w annałach historii jako jednego z najpotężniejszych praw natury, jako ostateczny rozbłysk w szeregu dokonań fali milenijnej.
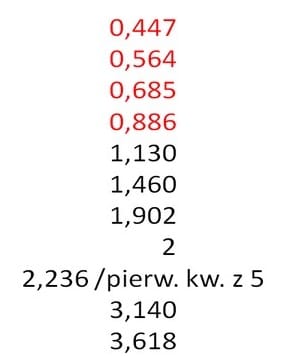
Potęga współczynnika 0.618:

Potęga współczynnika 1.618:
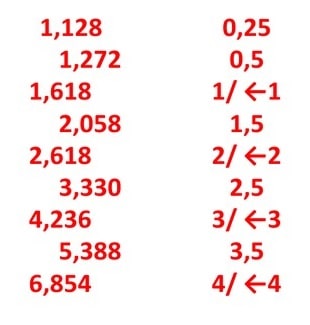
Inne współczynniki: