
Wracając do naszych rozważań na temat „nicnierobienia” i potrzebnych ku temu warunków zauważmy, że przeciętny osiemnastolatek dożyje w przybliżeniu 72, a jego rówieśnica 80 lat. Skoro wiemy już, ile czasu będziemy żyli, możemy ustalić, ile będzie nam potrzeba pieniędzy. Przyjmijmy więc, że na miesiąc chcemy dysponować kwotą 1000 zł i załóżmy przejście na emeryturę w wieku 40 lat. Przemnóżmy więc liczbę lat, jaka pozostała od emerytury do śmierci przez 12 miesięcy i przyjęte przez nas 1000 zł.
M : 1000 zł × 12 × 32 = 384 400 zł
K : 1000 zł × 12 × 40 = 480 000 zł
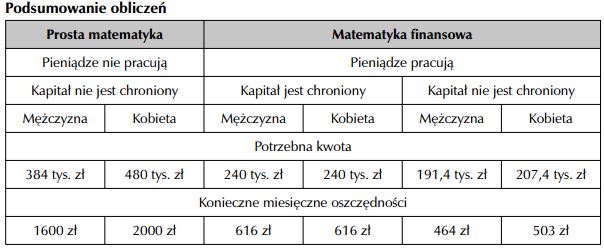
Dokonując bardzo prostego działania matematycznego, otrzymaliśmy nieco przygnębiający wynik. Aby przejść na emeryturę w wieku 40 lat i do końca życia dysponować kwotą 1000 zł miesięcznie, musimy uzbierać 384 tys. zł (jeżeli jesteśmy mężczyzną) lub 480 tys. zł (jeżeli jesteśmy kobietą). Odpowiedź uzyskaliśmy dzięki matematyce. Ale czy na pewno jest ona właściwa?
Należy jeszcze obliczyć, ile musimy oszczędzać, żeby zebrać potrzebną kwotę. Jeżeli założymy, że zaczniemy gromadzenie oszczędności w wieku 20 lat, to do upragnionej wcześniejszej emerytury w wieku lat 40 pozostaje nam 20 lat.
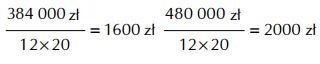
Wersja I
Na szczęście, odłożone przez nas pieniądze mogą pracować, np. mogą leżeć na bankowej lokacie, na której do kwoty kapitału co miesiąc dopisywane są odsetki. Ile pieniędzy potrzebujemy zgromadzić w takiej sytuacji? Tyle, by wysokość tych odsetek wynosiła dokładnie 1000 zł potrzebne nam co miesiąc. W ten sposób nie uszczuplając kwoty kapitału, moglibyśmy cieszyć się urokami życia na przyśpieszonej emeryturze. Jak obliczyć tę kwotę?
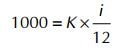
gdzie: i to roczna stopa procentowa.
Jeżeli przyjmiemy, że roczna stopa procentowa wynosi 5% i podstawimy ją do wzoru, to otrzymamy potrzebny nam wynik:
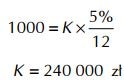
Aby co miesiąc wypłacać odsetki w wysokości 1000 zł i nie zmniejszać swojego majątku, musimy posiadać 240 tys. zł i ulokować je przy rocznej stopie procentowej równej 5%. Warto zauważyć, że w tym wypadku mamy pełne równouprawnienie. W tym wariancie zarówno mężczyzna, jak i kobieta potrzebuje dokładnie tyle samo pieniędzy.
Wersja II
Przedstawione poprzednie rozwiązanie posiada tę zaletę, że nie uszczupla naszego kapitału. Co miesiąc wypłacamy sobie 1000 zł, a na koncie cały czas pozostaje 240 tys. zł. Zastanówmy się jednak chwilę nad ludzkim przemijaniem i odpowiedzmy sobie na pytanie: po co nam 240 tys. zł w chwili śmierci. Non omnis moriar, jak powiedział poeta – ale czy na pewno chcemy sobie budować pomnik w postaci zapisu cyfr na rachunku bankowym? A gdybyśmy tak zechcieli pójść na całość i zakończyć żywot z całkowicie pustym kontem? Odpowiedź znów uzyskamy dzięki matematyce finansowej, posługując się wzorem na rentę płatną z dołu.
Renta płatna z dołu


Ile należy oszczędzać, żeby nic nie robić?
Jak można się domyślić, odpowiedź uzyskamy dzięki matematyce finansowej. Posłużymy się znanym wzorem na wartość przyszłą strumienia pieniędzy:

Posługując się kalkulatorem lub arkuszem kalkulacyjnym (nie jesteśmy przecież tak szaleni, by ręcznie liczyć sumę 240 iloczynów), dojdziemy do wyników:
- dla mężczyzny ok. 464 zł,
- dla kobiety ok. 503 zł.
Z naszych obliczeń wynika, że mężczyzna musi zacząć oszczędzanie w wieku 20 lat i przez następne 20 odkładać na konto (oprocentowane w wysokości 5% rocznie) co miesiąc 464 zł, by zgromadzić kwotę pozwalającą mu na wypłacanie sobie dożywotniej renty w wysokości 1000 zł. Kobieta, która rozpocznie oszczędzanie w takim samym wieku, przez następne 20 lat musi odkładać po 503 zł miesięcznie, by cieszyć się taką samą emeryturą jak mężczyzna.
Wyniki osiągnęliśmy dzięki matematyce finansowej, a intuicyjne zastosowanie prostej matematyki mogłoby poprowadzić nas na manowce.
Zastrzeżenia drobnym drukiem
Uwaga! Dokonując powyższych obliczeń, przyjęliśmy pewne założenia, które mogą mieć znaczący wpływ na ten wynik.
- Po pierwsze, przyjęta przez nas roczna stopa procentowa w wysokości 5% jest stopą nominalną. To znaczy, że nie uwzględnia inflacji. Innymi słowy, w warunkach inflacji dzisiejsze 1000 zł za kilka lat będzie warte już mniej. Aby zapewnić sobie w przyszłości emeryturę, za którą będziemy mogli kupić tyle samo co za 1000 zł, roczna realna stopa procentowa musi wynosić 5%, czyli musi być o 5 punktów procentowych wyższa od inflacji.
- Po drugie, podawane przez Główny Urząd Statystyczny długości życia są średnie dla całej populacji. Nie bierzemy odpowiedzialności za ewentualne dłuższe bądź krótsze życie Czytelników. Należy więc zatem ostrożnie liczyć potrzebne nam na emeryturę kwoty, by nie wyczyścić sobie konta wcześniej niż pisana nam rzeczywiście data śmierci.

















