
Geometria rynku opiera się głównie na porównaniu odcinków, które tworzą lokalne szczyty i dołki cenowe ze sobą. Do porównań wykorzystywana jest analiza cen i czasu, a wykorzystanie geometrii rynku pozwala na zbadanie zależności zarówno w trendach wzrostowych jak i spadkowych na dowolnym wykresie instrumentu finansowego. Wykorzystując ciąg Fibonacciego do handlu na giełdzie lub na rynku forex wykorzystujemy tylko wysokości odcinków, a nie ich nachylenie.
Geometria rynku wywodzi się od włoskiego matematyka znanego jako Leonardo Fibonacci. Żył on na przełomie XII i XIII wieku. Dzięki niemu europejski matematyk, po wielu latach zastoju zaczęła się odradzać na nowo. Jego głównym odkryciem jest sekwencja numeryczna powszechnie określana jako ciąg Fibonacciego.
Kolejność liczb naturalnych, które odkrył Fibonacci, jest następująca:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181
Zależności ciągu Fibonacciego :
- Ciąg zaczyna się od liczby 1 i 1. Każdy kolejny numer ciągu jest sumą dwóch poprzednich liczb.
- Iloraz liczby ciągu i liczby poprzedniej wynosi 1.618, a iloraz kolejnej liczby po tej liczbie wynosi 0,618.
- Stosunek między dwoma liczbami oddalonymi o 2 miejsca wynosi 2.618 oraz odwrotnie, czyli 0.382.
Sposób, w jaki możemy wyliczyć współczynniki Fibonacciego:
- 1 ÷ 1.618 = 0.618
- 0.618 × 0.618 = 0.382
- 1.618 × 1.618 = 2.618
- 2.618 × 1.618 = 4.236
- 1 – 0.618 = 0.382
- 1.618 ÷ 0.618 = 2.618
- 0.618 ÷ 1.618 = 0.382, itd.
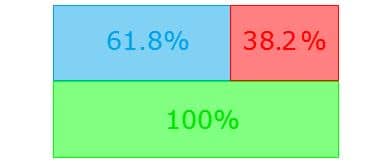
Ze wszystkich współczynników Fibonacciego, 0,618 i 1,618 odgrywają najważniejszą rolę. 1,618 jest również znany jako liczba Phi. Liczba Phi pokazuje złoty podział, który został przedstawiony na poniższym rysunku. Jest to podział odcinka w taki sposób, że stosunek dłuższego do krótszego odcinka (niebieski do czerwonego) jest taki sam jak suma dwóch odcinków do odcinka dłuższego (zielony do niebieskiego).
Wzór: 61.8 % : 38.2 % = 100 % : 61.8 % = 1.618
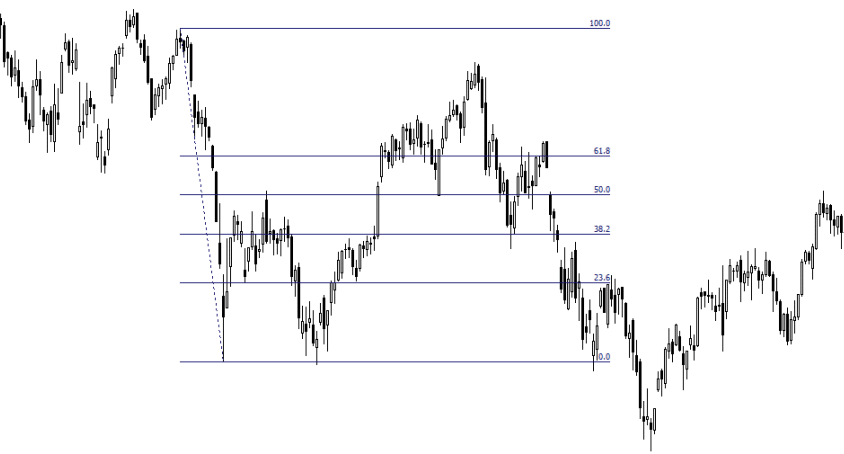
Poniższe poziomy są najczęściej stosowane w handlu harmonicznym na giełdzie i pochodzą z ciągu Fibonacciego, jak również z innych proporcji matematycznych: Podstawowe poziomy: 38,2%, 50%, 61,8%, 100%, 127,2%, 161,8%, 200%, 261,8%, 361,8% Dodatkowe poziomy: 23,6%, 70,7%, 78,6%, 88,6%, 113%, 141,4%, 223,6%, 314%
Proporcje wynikające z sekwencji numerycznej odkrytej przez Fibonacciego można zaobserwować w naturze. Są to na przykład: tarcze słonecznika, różyczka kalafiora, owoc ananasa, gdzie układ spirali wynika z ciągu Fibonacciego. U większości roślin łodygi, liście i kwiaty rozwijają się pod kątem, który można obliczyć na podstawie numerów tej sekwencji.
Przykładem występowania liczby Phi, która również wynika z sekwencji, jest struktura ciała ludzkiego. Rzucając proporcje (0,382 i 0,618) na ludzką twarz, uzyskalibyśmy złote centrum w postaci linii oczu. Innym przykładem jest wzrost człowieka. Stosując złoty środek dowiedzielibyśmy się, że pępek znajduje się na granicy tych proporcji. Innym przykładem jest nasza ręka, gdzie łokieć jest złotym środkiem, mierząc długość ręki od ramienia do końca palców. Liczby Fibonacciego można zobaczyć wszędzie. Warto wspomnieć o spirali logarytmicznej, która rozwija się lub kurczy w oparciu o współczynnik 1,272, który jest elementem z liczby Phi.
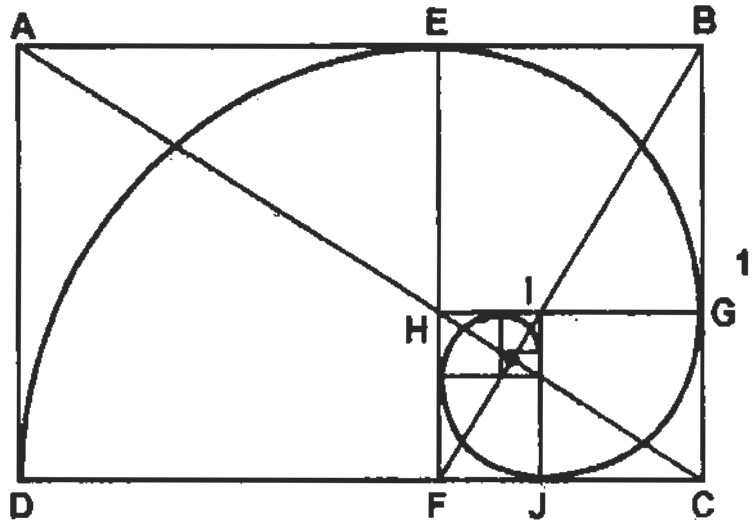
Kształt spirali równobocznej można opisać za pomocą złotego podziału i liczb Fibonacciego. Każdy bok kwadratu wynikający z podzielonej spirali (patrz rysunek powyżej) w stosunku do kolejnych boków odpowiada sekwencji Fibonacciego. Tak więc, od środka, każdy kolejny bok kwadratu będzie się zwiększał, a stosunek ten będzie się zwiększał w tym samym stopniu, co numery wspomnianego ciągu (1,1,2,3,5,…).