Podstawowymi determinantami każdej inwestycji na rynku kapitałowym są stopa zwrotu i ryzyko. Niestety zwiększonym zyskom towarzyszy większe ryzyko. Oba parametry można oszacować metodami matematycznymi.
Stopa zwrotu
Stopa zwrotu jest jednym z podstawowych parametrów opisujących jakość inwestycji w instrumenty finansowe. Oblicza się go jako stosunek osiągniętego zysku do poniesionych nakładów inwestycyjnych. Niestety, nikt nie może zdecydowanie określić przyszłej stopy zwrotu. Dlatego są one szacowane z uwzględnieniem wyników historycznych.
W przypadku akcji stopę zwrotu za dany okres oblicza się według wzoru:
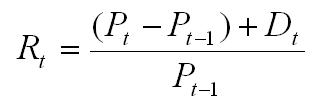
gdzie:
Rt – stopa zwrotu za okres „t”
Pt – cena akcji na koniec okresu „t”
Pt-1 – cena akcji na koniec poprzedzającego okresu
Dt – dywidenda wypłacona w okresie „t”
Przykład 1.
Na początku roku inwestor (A3) kupił jedną akcję (A4) Alfa po 15,80 PLN. Na koniec roku kurs wymiany (A13) wzrósł do 21,40 PLN. Jednocześnie w ciągu roku spółka wypłaciła dywidendę (A5) w wysokości 0,60 PLN na akcję. Stąd stopa zwrotu z inwestycji za rok wyniosła:
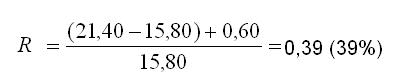
Przy wyznaczaniu oczekiwanej stopy zwrotu, którą można uzyskać z danego papieru wartościowego (A2), zakłada się, że jest to zmienna losowa, a jej wartość zależy od prawdopodobieństwa spełnienia określonych scenariuszy, które mogą wystąpić na rynku. Oczekiwaną stopę zwrotu oblicza się ze wzoru:
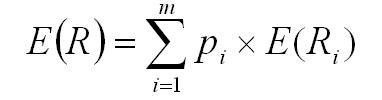
gdzie:
E(R) – oczekiwana stopa zwrotu
pi – prawdopodobieństwo wystąpienia danej stopy zwrotu w scenariuszu „i”
E(Ri)– oczekiwana stopa zwrotu przy scenariuszu „i”
m – ilość scenariuszy sytuacji na rynku
Przykład 2.
Szacujemy oczekiwaną stopę zwrotu na następny rok akcji Alfa. Zakładając, że w dobrej sytuacji rynkowej przyniesie zysk w wysokości 20%, w średniej sytuacji 10%, aw przypadku recesji strata w wysokości 8%. Prognozy ekonomistów pokazują, że prawdopodobieństwo dobrych warunków rynkowych wynosi 0,5, średnio 0,2, a źle 0,3.
Stąd oczekiwana stopa zwrotu akcji spółki Alfa wynosi:
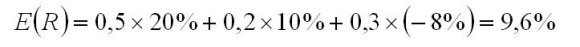
Oczekiwaną stopę zwrotu można również obliczyć na podstawie historycznych stóp zwrotu. Następnie użyj następującej formuły:
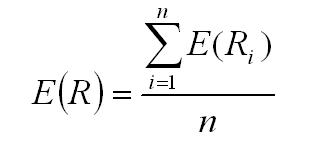
gdzie:
n – ilość historycznych stóp zwrotu (np. sesji)
Przykład 3.
Akcje Gamma osiągnęły następujące stopy zwrotu w ciągu ostatnich 5 sesji:
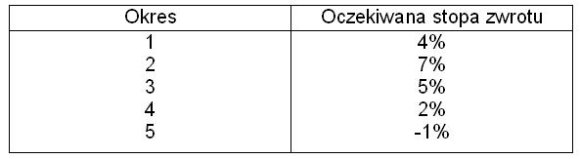
Zatem oczekiwana stopa zwrotu jest średnią arytmetyczną wszystkich stóp zwrotu w tym okresie.
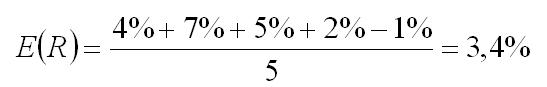
Oczekiwana stopa zwrotu z portfela aktywów, np. akcje, jest średnią oczekiwanych stóp zwrotu ważonych udziałami poszczególnych składników tego portfela.
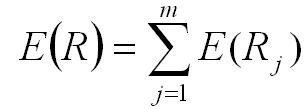
gdzie:
E(Rj)– oczekiwana stopa zwrotu akcji spółki „j”
Przykład 4.
Inwestor zainwestował w akcje trzech spółek A, B, C. Ich akcje i oczekiwane stopy zwrotu są następujące:

Dlatego oczekiwana stopa zwrotu z tak zbudowanego portfela wynosi:
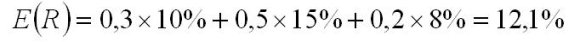
Ryzyko papierów wartościowych
Ryzyko jest nieodłącznie związane z inwestycjami na rynku kapitałowym (A2). Jest to drugi podstawowy parametr charakteryzujący inwestycję, determinujący decyzje podejmowane przez inwestorów (A3). Innymi słowy, ryzyko to niepewność co do przyszłej stopy zwrotu. Zwiększa się wraz ze zmiennością stóp zwrotu i nie ma znaczenia, czy są to zmiany pozytywne czy negatywne.
Miarą ryzyka jest wariancja stopy zwrotu z papierów wartościowych (A2). Można to obliczyć za pomocą wzoru:
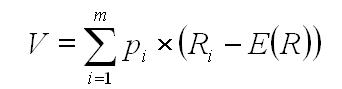
gdzie:
V – wariancja stopy zwrotu;
pi – prawdopodobieństwo wystąpienia danej stopy zwrotu;
Ri – możliwa do uzyskania stopa zwrotu z danym prawdopodobieństwem.
Odchylenie standardowe stopy zwrotu jest kolejną i najczęściej stosowaną miarą ryzyka. Matematycznie jest to pierwiastek kwadratowy wariancji.
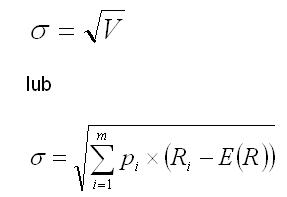
Przykład 5.
Akcje dwóch spółek X i Y mają różne stopy zwrotu w każdej z możliwych sytuacji na giełdzie: hossy (C1), konsolidacji, bessy (C1). Tabela podsumowuje stopy zwrotu, które charakteryzowały te udziały (A4) w przeszłości. Określono prawdopodobieństwo każdego scenariusza na giełdzie.
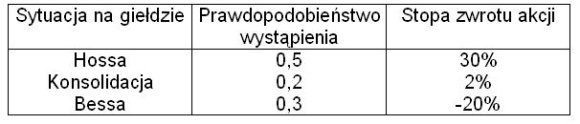
tabela1

Jeżeli do obliczenia wariancji i odchylenia standardowego wykorzystywane są dane z przeszłości, należy zastosować następujące wzory:
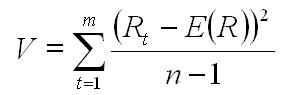
Jednak standardowe odchylenie stóp zwrotu określa wzór:
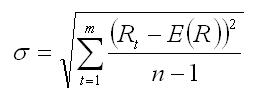
Przykład 6.
Obliczmy wariancję i odchylenie standardowe stóp zwrotu dla danych z przykładu 3.
Po podstawieniu do formuły 7 otrzymujemy:

Współczynnik zmienności
Wybór najlepszej inwestycji w akcje (A4) na podstawie stóp zwrotu i odchyleń standardowych może często być trudny ze względu na duży rozrzut tych danych.
Dlatego do analizy wykorzystywany jest współczynnik zmienności. Reprezentuje stosunek ryzyka do zysku danego papieru wartościowego (A2), a zatem wskazuje, jakie ryzyko istnieje na jednostkę zwrotu. Jest to określone przez wzór:
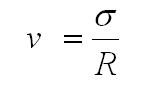
Przykład: Do obliczenia współczynnika zmienności wykorzystamy dane z przykładu 4. Po podstawieniu otrzymujemy:
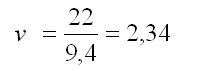
Im wyższy współczynnik zmienności, tym większe ryzyko zwrotu z inwestycji w dane papiery wartościowe.
Przykład 7.
Inwestor (A3) stoi przed problemem wyboru zakupu akcji jednej z trzech spółek: A, B, C. Ma również dane za ostatni rok i zakłada, że w przyszłości stopy zwrotu i ryzyko związane z inwestowaniem w tych udziałach będą takie same. Akcje dwóch spółek mają takie same stopy zwrotu i takie samo ryzyko.

Pytanie o to, które akcje należy wybrać, zostanie podane poprzez obliczenie współczynników zmienności.
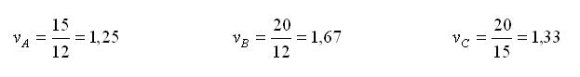
Jak widać, najniższym ryzykiem w stosunku do stopy zwrotu są obciążone akcje spółki A. Inwestor powinien inwestować w tę spółkę, mimo że jej akcje nie mają najwyższej stopy zwrotu z prezentowanej grupy.
Współczynnika zmienności nie można stosować przy porównywaniu różnych rodzajów instrumentów finansowych, np. akcje i obligacje (A8). Obligacje, zwłaszcza obligacje skarbowe (A15), mają ryzyko bliskie zeru, dlatego porównanie ich z akcjami zawsze prowadzi do jednego wniosku – inwestuję w obligacje. Dlatego wskaźnik ten jest cennym narzędziem przy podejmowaniu decyzji inwestycyjnych na giełdzie. Należy zauważyć, że współczynnik zmienności nie ma zastosowania do zwrotów ujemnych.
Korelacja stóp zwrotu
Korelacja to inna zależność między stopami zwrotu z dwóch różnych papierów wartościowych (A2). Stopień powiązania dwóch działań mierzy się za pomocą współczynnika korelacji Pearsona.
Jeżeli obliczenia zakładają prawdopodobieństwo pewnej stopy zwrotu z akcji (A4), wówczas stosuje się następujący wzór:
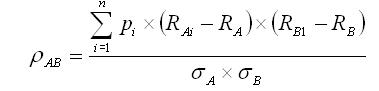
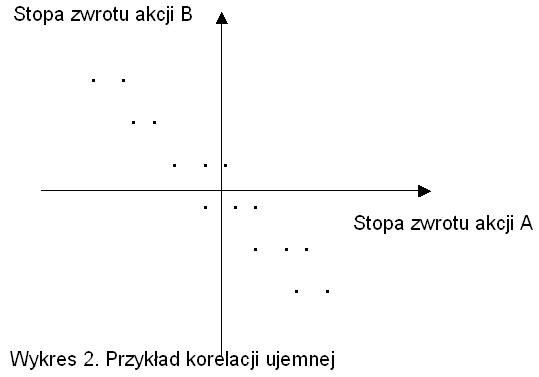
Współczynnik korelacji przyjmuje wartości z zamkniętego zakresu <-1; +1>. Znak (+) współczynnika korelacji wskazuje na dodatnią korelację akcji. Następnie wzrostowi stopy zwrotu z jednej akcji towarzyszy wzrost stopy zwrotu z drugiej akcji. Znak (-) współczynnika świadczy o ujemnej korelacji, co oznacza, że wzrost zwrotu z jednej akcji odpowiada spadkowi zwrotu z drugiej akcji.
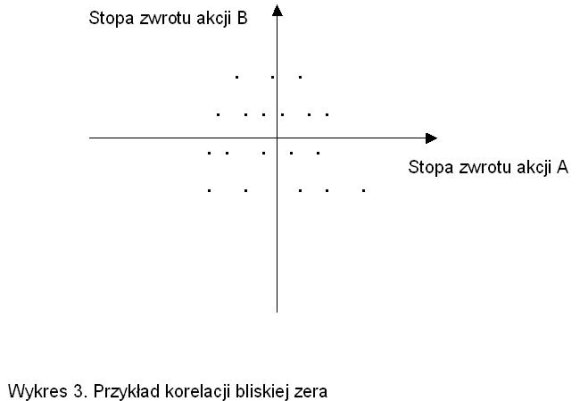
Im wyższa wartość bezwzględna współczynnika korelacji, tym większy stopień powiązania między stopami zwrotu. Aktywa są najsilniej powiązane, jeśli współczynnik korelacji jest bliski +1 lub -1, co oznacza wysoką korelację dodatnią lub ujemną. Nie mówi się o korelacji, gdy współczynnik korelacji jest bliski zeru lub równy zeru. Najczęściej na rynku akcji występuje dodatnia korelacja, która zwiększa się jeszcze bardziej podczas panicznej wyprzedaży akcji, charakterystycznej dla bessy (C1). Aktywa o różnych klasach, takie jak akcje i złoto (H3), wykazują ujemną korelację.
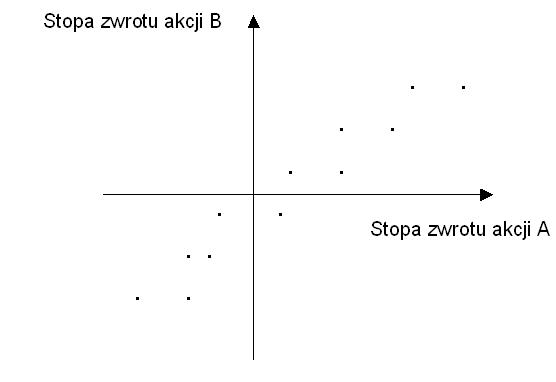
Wykres 1. Przykład korelacji dodatniej
Kowariancja to kolejna miara siły powiązania między zwrotami. Jego wartość zależy od zmienności stóp zwrotu. Podobnie jak w przypadku korelacji, można ją obliczyć przy użyciu prognoz przyszłych stóp zwrotu lub wyników historycznych. W tym celu stosuje się wzory.
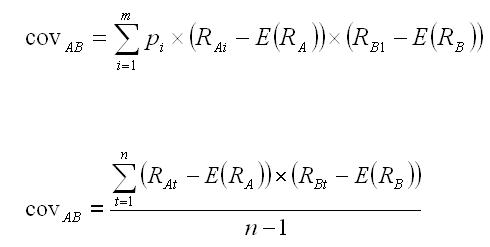
Tworzona jest symetryczna macierz kowariancji, aby zilustrować relacje wielu działań. Na przykład dla czterech akcji A, B, C, D wygląda to tak:
Wartości kowariancji leżące po przekątnej w macierzy są wariancją stóp zwrotu, ponieważ są kowariancją dwóch takich samych udziałów.
Istnieje następująca zależność między współczynnikiem kowariancji a współczynnikiem korelacji:
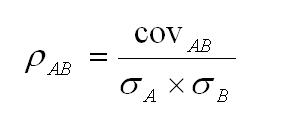
Dlatego znając kowariancję i odchylenia standardowe, można określić współczynnik korelacji zwrotów między dwoma instrumentami finansowymi. Omówione powyżej miary pozwalają na budowę portfela, w którym kryteriami wyboru aktywów są stopy zwrotu i ryzyko – ta metoda wyboru portfela jest stosowana w analizie portfela.

















