Zmniejszanie i zwiększanie prawdopodobieństwa remisu w piłce nożnej
- Jak działa model Poissona?
- Ograniczenia modelu Poissona
- Jak zwiększyć lub zmniejszyć prawdopodobieństwo remisu
Jednym z ograniczeń związanych z modelem Poissona jest brak wystarczającej skuteczności w wyznaczaniu prawdopodobieństwa wystąpienia bezbramkowych remisów. W tym artykule wyjaśniono, w jaki sposób dostosować model Poissona, aby lepiej uwzględniał bezbramkowe remisy. Przeczytaj artykuł, aby dowiedzieć się więcej.
Podstawowym modelem używanym do przewidywania wyników w piłce nożnej jest model Poissona (lub jego warianty). Najprostszy sposób polega na określeniu parametru oczekiwanej liczby bramek dla każdej drużyny, na podstawie którego będą przewidywane wyniki.
W modelu Pooissona parametrem drużyny gospodarzy jest ligowa średnia bramek zdobywanych u siebie pomnożona przez współczynnik ataku drużyny gospodarzy oraz współczynnik obrony drużyny gości. Pierwszy współczynnik określa przewagę własnego boiska, natomiast drugi współczynnik dotyczy możliwości strzelenia bramki przyjezdnym (im silniejsza ich obrona, tym mniejsza szansa na strzelenie gola). Wskaźnik oczekiwanej liczby bramek drużyny gości jest oceniany w podobny sposób, z tym że w tym przypadku używa się współczynników ataku gości i współczynników obrony gospodarzy.
Chciałbyś uniknąć przegranej z powodu remisu? Dowiedz się jak działa bukmacher DNB!
Ograniczenia modelu Poissona
Każdy model jest obarczony pewnymi ograniczeniami. To samo dotyczy modelu Poissona wykorzystywanego do przewidywania rezultatów meczów piłki nożnej, w którym to wyniki są wrażliwe na zmiany użytych parametrów.
„Prawdopodobieństwo zremisowania 0:0 jest znacznie wyższe w przypadku drużyn zdobywających dużo bramek, ponieważ mogą one zwolnić tempo gry w sytuacji, gdy mecz pozostaje bezbramkowy po upływie znacznego czasu od jego rozpoczęcia.”
Model Poissona zakłada również, że gdy ustalali się już parametry oczekiwanej liczby bramek, to liczby goli zdobywanych przez oba zespoły są od siebie niezależne. Rzeczywiście do pewnego stopnia jest to kontrolowane za pomocą specjalnych wskaźników dotyczących obrony i ataku. Czy jednak naprawdę możemy oczekiwać, że prawdopodobieństwo zdobycia pięciu bramek przez drużynę gości będzie tak samo niezależnie od tego, czy drużyna gospodarzy zdobędzie pięć goli, czy też żadnego?
Największym ograniczeniem jest założenie charakteryzujące rozkład Poissona, w którym wariancja liczby bramek zdobytych przez drużynę jest równa oczekiwanej liczbie bramek. Istnieją sprytne sposoby radzenia sobie z tym problemem. Przykładem mogą być złożone (lub uproszczone) modele Poissona oraz model Poissona bazujący na dwóch zmiennych, jednak omówienie ich wykracza poza zakres tego artykułu.
Jednym ze skutków tych ograniczeń jest brak skutecznej oceny prawdopodobieństwa wystąpienia remisu 0:0, które może być wyższe lub niższe od wyniku otrzymanego po zastosowaniu modelu Poissona. W moim przekonaniu model Poissona ma tendencję do zaniżania prawdopodobieństwa remisu 0:0 w przypadku drużyn o wysokich parametrach oczekiwanej liczby bramek.
Prawdopodobieństwo zremisowania 0:0 jest znacznie wyższe w przypadku drużyn zdobywających dużo bramek, ponieważ mogą one zwolnić tempo gry w sytuacji, gdy mecz pozostaje bezbramkowy po upływie znacznego czasu od jego rozpoczęcia. Z kolei drużyny strzelające mało bramek mogą narzucać szybsze tempo gry do momentu zdobycia pierwszego gola. Standardowy model Poissona nie uchwyciłby tego zachowania, a tym samym błędnie oceniłby szansę remisu 0:0. Należy jednak pamiętać, że jest to tylko moje spostrzeżenie, które nie zostało udowodnione w żaden sposób. Gdyby jednak ktoś zechciał przeprowadzić badanie tego tematu, to zachęcam do kontaktu ze mną.
Jak zwiększyć lub zmniejszyć prawdopodobieństwo remisu
Jednym ze sposobów na odpowiednie ustalenie prawdopodobieństwa wystąpienia remisu 0:0 jest zwiększenie lub zmniejszenie prawdopodobieństwa takiego zdarzenia i odpowiednie skorygowanie innych prognoz. Poniżej opisaliśmy pięć kolejnych kroków tego procesu, posługując się prostym przykładem.
Krok 1: Obliczanie parametrów oczekiwanej liczby bramek dla poszczególnych drużyn
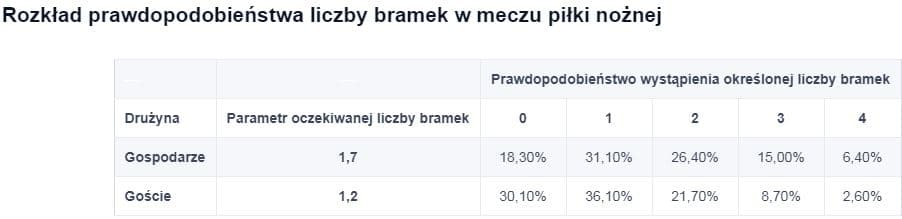
Jest to chyba najbardziej pracochłonny etap, o ile nie udało się go zautomatyzować. Aby zachować zwięzłość niniejszego artykułu przyjmiemy, że ostateczne średnie parametry bramek to 1,7 dla gospodarzy i 1,2 dla gości (podane liczby są przypadkowe).
Krok 2: Obliczanie prawdopodobnej liczby bramek do zdobycia przez poszczególne drużyny
Te obliczenia można dokonać za pomocą wzoru. Aby zobaczyć przykład wystarczy kliknąć powyższy link. W tym przypadku używamy rozkładu prawdopodobieństwa dla liczby zdobytych bramek na podstawie następującego wzoru:
Krok 3: Obliczanie rozkładu prawdopodobieństwa dla określonego wyniku meczu
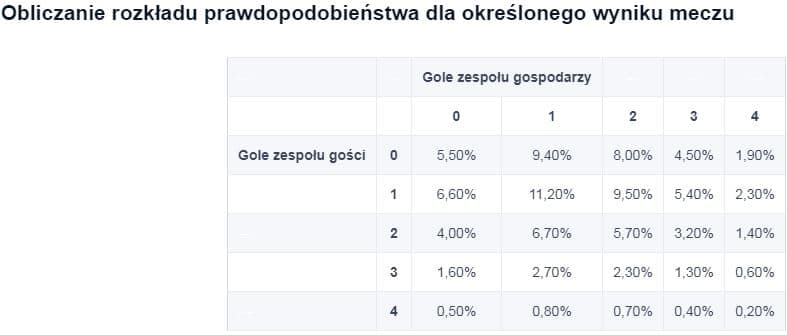
Teraz możemy pomnożyć prawdopodobieństwa dla różnych wyników. Na przykład prawdopodobieństwo otrzymania wyniku 0:0 wynosi 18,3% x 30,1% = 5,5%. Rezultaty dokonanych obliczeń będą wyglądać jak pokazano poniżej. Należy pamiętać, że suma otrzymanych wyników nie będzie wynosić 100%, ponieważ istnieje możliwość zakończenia meczu innymi wynikami (na przykład 5:1). Warto dodać, że prawdopodobieństwo otrzymania innych wyników w meczu wynosi 3,7%.
Krok 4a: Obliczanie parametru zwiększającego/zmniejszającego dla remisu 0:0
Na tym etapie może pojawić się pewien stopień subiektywnej oceny. Załóżmy na przykład, że wcześniejsze statystyki sugerują 10% prawdopodobieństwo remisu 0:0. W takiej sytuacji należałoby zwiększyć uzyskaną w kroku 3 wartość 5,5% do 10%.
Parametr zwiększający prawdopodobieństwo można obliczać następująco:
(domniemane prawdopodobieństwo remisu 0:0)/(przewidywane prawdopodobieństwo)=(domniemane prawdopodobieństwo)/(prawdopodobieństwo(0,0))
Zastępując ten zapis symbolem α, otrzymamy:
α=10/5,5=1,82.
Oznacza to, że zwiększamy prawdopodobieństwo bezbramkowego remisu o 82%. Ponieważ prawdopodobieństwo wzrosło z 5,5% do 10%, suma pozostałych prawdopodobieństw musi zostać zmniejszona o tę samą wartość procentową, tak aby całkowity odsetek wszystkich otrzymanych wyników wynosił 100%.
Krok 4b: Obliczanie parametru zwiększającego/zmniejszającego dla innych wyników
W tym przypadku użyjemy symbolu β i skorzystamy z następującego równania:
β=(1-α[prawdopodobieństwo(0,0)])/(1-[prawdopodobieństwo(0,0)])=(1-domniemane prawdopodobieństwo)/(1-przewidywane prawdopodobieństwo)
Otrzymamy następujący wynik β=(1-0,1)/(1-0,055)=0,95
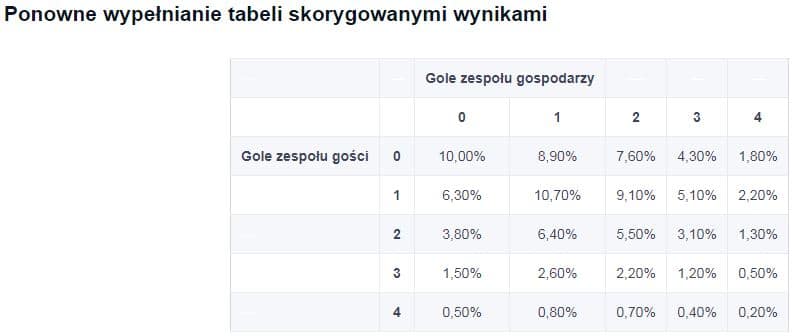
Krok 5: Ponowne wypełnianie tabeli skorygowanymi wynikami
Teraz możemy ponownie obliczyć prawdopodobieństwa dla różnych wyników, mnożąc prawdopodobieństwo remisu 0:0 przez α, a pozostałych rezultatów przez β. Otrzymalibyśmy następujące wyniki, przy czym prawdopodobieństwo zakończenia meczu innym wynikiem wynosi 3,5%.
Czego dowiedzieliśmy się o dostosowywaniu modelu Poissona?
W niniejszym artykule omówiliśmy możliwość dostosowania typowego modelu Poissona, który zmienia prawdopodobieństwo wystąpienia bezbramkowego remisu. Model ten można rozszerzyć o możliwość dostosowania dowolnego wyniku, o ile łączne prawdopodobieństwo wystąpienia wszystkich wyników zostanie skorygowane do wartości 100%.
Nie jest to jedyny sposób dokonania zmiany prawdopodobieństwa wystąpienia określonych wyników meczu. Podczas konferencji MathSport w czerwcu zeszłego roku dr Alun Owen objaśnił działanie innego podejścia (prawdopodobnie lepszego), które dotyczyło skróconego modelu Poissona.
Wprowadzona przez niego korekta nie minimalizuje jednak ograniczeń modelu Poissona, które zostały częściowo omówione wcześniej. Za to wprowadza założenia dotyczące prawdopodobieństwa wystąpienia wyniku bezbramkowego oraz dostosowania wszystkich innych prawdopodobieństw za pomocą tego samego wskaźnika β. Mimo wszystko może to ulepszenie względem tradycyjnych modeli, które mają tendencję do traktowania bezbramkowych remisów za zbyt mało lub zbyt bardzo prawdopodobne.