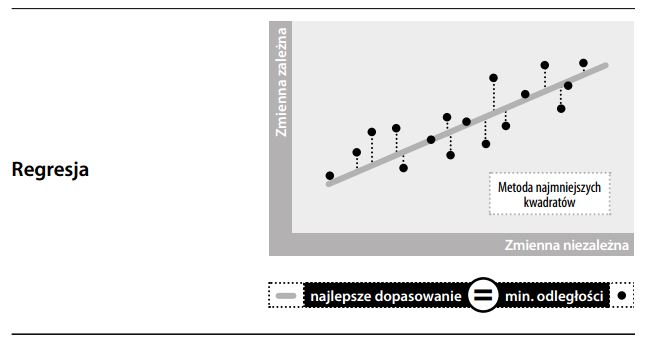
Analiza regresji/Technika najmniejszych kwadratów (w szacunku kosztów)
Technika statystyczna służąca do wywnioskowania przyszłego kształ- towania się kosztów w reakcji na zmiany zmiennej przyczynowej (nośnika kosztu). W celu ustalenia stosunku pomiędzy zmienną zależną (zwykle kosztami łącznymi) a grupą kształtujących koszty zmiennych niezależnych (np. nakładów produkcyjnych, wydajności produkcji, poziomu produkcji) wykorzystuje się dane historyczne. Po rozwiązaniu równania (zob. poniżej), możemy je zastosować do prognozowania przyszłych kosztów łącznych (zakładając, że przyjęte relacje będą nadal istniały w przyszłości). Miarodajność prognoz można zmierzyć stopniem pokrywania się obserwacji z równaniem liniowym. „Współczynnik determinacji” mówi analitykom, jaką część procentową zmian kosztów można przypisać do danego nośnika kosztów.
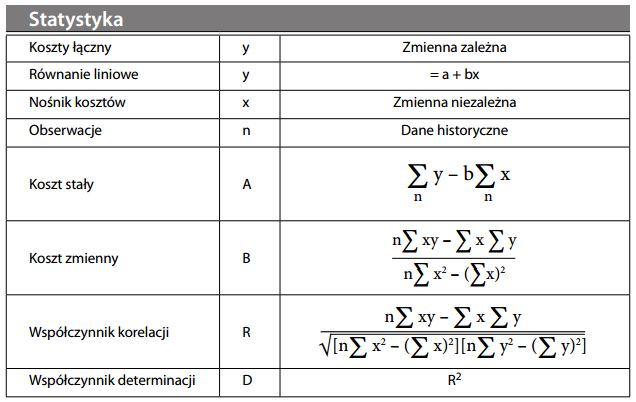
Wysoki współczynnik determinacji (R2 wynoszący np. ponad 80%) sugeruje, choć nie dowodzi, że występuje związek przyczynowy. Choć analiza regresji jest elegancka i wyszukana, nie możemy zapominać o ostrzeżeniu, jakie miał wypowiedzieć Mark Twain („Istnieją trzy rodzaje kłamstwa: kłamstwa, wierutne kłamstwa i statystyka”.). Przykładowo, związek przyczynowy może być jedynie pozorny (sprzedaż lodów i sprzedaż okularów przeciwsłonecznych też mogą być ze sobą skorelowane, ale łącznikiem przyczynowym jest faktycznie pogoda, która wpływa na wielkość sprzedaży obu tych artykułów). By móc wyciągać wnioski, należy mieć wystarczającą ilość przeprowadzonych obserwacji. Dokonywanie ekstrapolacji w oderwaniu od obserwacji jest zawsze ryzykowne, ponieważ mogą występować różne relacje. Z zastrzeżeniem powyższych uwarunkowań, analiza regresji przesuwa rachunek kosztów z pola sztuki na pole nauki.